zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite
7. Modellrechnungen zur Schwerewirkung von Mantel-Plume-Hot-Spot-
Strukturelementen
Aus der Klassifizierung (Kap. 4) ist die Beobachtung hervorgegangen, daß Mantel-Plume-Hot-Spots offenbar von einer topographischen Schwelle regionalen Ausmaßes umgeben sind. Vermutete ursächliche Zusammenhänge für die Hot Spots im allgemeinen und für die Mantel-Plume-Hot-Spots im besonderen wurden bereits in den Kapiteln 4.3.2. bzw. 2.2.2. diskutiert. Unabhängig hiervon ist noch nicht untersucht worden, wie es überhaupt zur Ausbildung von Hot-Spot-Schwellen kommt. Die Schwellenbildung um die Mantel-Plume-Hot-Spots ist bisher lediglich als Beobachtung festgestellt worden. Als Ursache für die Mantel-Plume-Hot-Spots wird eine Mantel-Plume-Struktur angegeben. Inwieweit diese Struktur aber zur Bildung der Schwelle beiträgt, darüber liegt noch keine Aussage vor. Die Schwellenbildung kann sowohl eine unmittelbare Folge der Mantel-Plume-Aktivität sein, sie kann aber auch durch sekundäre Prozesse, also als Folge einer oder mehrerer Folgen von Mantel-Plume-Ursachen entstehen. Fest steht offenbar nur, daß diese Schwellung in irgendeiner Weise zumindest indirekt durch die Mantel-Plume-Struktur hervorgerufen wird.
7.1. Mögliche Ursachen der Hot-Spot-Schwellenbildung
7.1.1. Flexur der Kruste, veränderte Lithosphäre und Plume
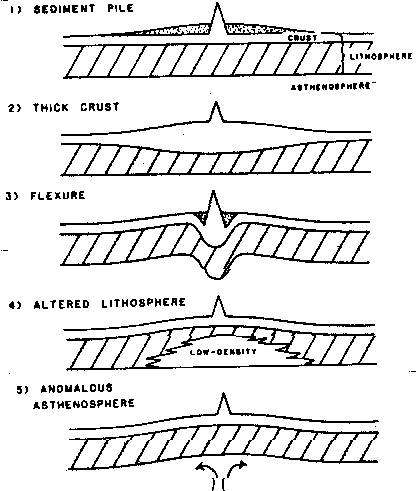
Verschiedene Vorschläge über die Ursachen der Schwellenbildung, wohlgemerkt nicht gleichzusetzen mit der (Mantel-Plume)-Hot-Spot-Bildung, gibt es in der Literatur. Crough (1983a) hat diese Vorstellungen zusammengefaßt und in fünf Kategorien eingeteilt, die die Abb. 54 zeigt.
Lancelot et al. (1977) schlug die Akkumulation von Sedimenten (Abb. 54a) als Ursache für die Schwellen um Hot Spots vor. Obwohl nach Menard (1964) Sedimente sich in Ablagerungsräumen vulkanischer Förderprodukte verdik-ken, kann dieser Mechanismus nicht zur Erklärung der Schwellen herangezogen werden. Sowohl Bohrungen als auch reflexionsseismische Untersuchungen am Kapverden-Hot-Spot (Lancelot et al., 1977) zeigen, daß das Basement angehoben worden ist. Darauf weisen auch die in Kapitel 5 gezeigten, aus seismischen Messungen und gravimetrischen Modellrechnungen (Dichtemodel-le) abgeleiteten Krustenprofile über Hawaii hin. In diesem Sinne kommt die Möglichkeit einer regionalen Sedimentakkumulation als Ursache nicht in Frage.

Abb. 54. Modellvorstellungen für Hot-Spot-Schwellen nach Crough (1983a).
a) Anhäufung von Sedimenten,
b) verdickte Kruste,
c) Flexur,
d) altered (veränderte) Lithosphäre verminderter Dichte,
e) anomale Asthenosphäre.
Betz und Hess (1942) versuchen, die Hawaii-Schwelle durch von den Vulkaninseln ausgehende Lavaflüsse zu erklären. Wiederholtes Auftreten solcher Lavaflüsse führt über geologische Zeiträume hinweg zur Verdickung der ozeanischen Kruste (Abb. 54b). Damit wäre also die Schwelle, wie auch übrigens im ersten Falle, als Folge der vulkanischen Tätigkeit zu erklären. Sowohl die Ergebnisse in Kapitel 5 als auch z. B. Shor und Pollard (1964) zeigen auf, daß die Kruste unter der Hawaii-Schwelle eine im wesentlichen einheitliche Mächtigkeit aufweist. Eine Ausnahme liegt lediglich in der unmittelbaren Umgebung der Inseln vor, die aber in ihrer Ausdehnung nicht mit der regionalen Schwelle in Beziehung gesetzt werden kann. Daher kann als Schwellenursache auch keine wie auch immer entstandene verdickte Kruste angenommen werden.
Walcott (1970b) erklärte die Hawaii-Schwelle durch Flexur (Abb. 54c), die durch die vulkanische Auflast bedingt ist. Danach wird die Kruste unter den Inseln eingedrückt und in einer bestimmten Entfernung hochgebogen. Formalismen zur Berechnung von Flexur und Stress auf elastische Lithosphäre erarbeiteten z. B. Turcotte (1979) oder Solomon und Head (1979). Auf deren Überlegungen wird in der vorliegenden Arbeit im folgenden durch den Terminus "Balkenbiegetheorie" verwiesen. Damit können Größe und Form der Schwelle zwar erklärt werden, jedoch ist die Freiluftanomalie damit nicht kompatibel, was die folgenden Überlegungen zeigen.
Unter einer seitlichen Krustenaufwölbung durch Flexur infolge der vulkanischen Auflast liegen keine Massendefizite für einen isostatischen Ausgleich. Somit ergibt sich nach Crough (1983a) eine Freiluftanomalie mit einer Amplitude von 2 h, wobei die Gravitationskonstante, der Dichtekontrast zwischen aufgewölbtem Material und Umgebung (hier Wasser) und h die Höhe der Aufwölbung ist. Daraus ergibt sich ein Wert von etwa 90 mGal für eine ein Kilometer hoch aufgewölbte Kruste in marinen Bereichen (Watts und Talwani, 1974). Nach Watts (1976) und Detrick und Crough (1978) liegt der Wert für dieses Schwere-Tiefen-Verhältnis für Hawaii nur bei ca. 20 bis 25 mGal/km. Der Erwartungswert von ca. 90 mGal/km (Crough, 1977; Watts und Talwani, 1974), beobachtet an Flexuren bei Subduktionsprozessen, kann bei Hawaii nicht nachgewiesen werden.
Die Modelle nach Abb. 54a,b,c versuchen, die Schwelle durch krusteninterne, also "flache" Ursachen zu erklären. Lediglich im dritten Fall kann ein nicht zu vernachlässigender Beitrag zur Schwellenursache nicht ausgeschlossen werden. Jedoch sind die in Kapitel 5 zur Krustenmodellierung herangezogenen Schwerewerte nicht alleinig durch Flexur erklärbar. Die Schwellenbildung muß offenbar tiefer gelegene Ursachen haben.
Die tiefergelegenen möglichen Schwellenursachen lassen sich in zwei Gruppen einteilen:
- Lage der Ursache innerhalb der Lithosphäre,
- Lage im sublithosphärischen Bereich bzw. der Asthenosphäre.
Keine der beiden Möglichkeiten kann im Gegensatz zu Abb. 54a und Abb. 54b als in Frage kommende Schwellenursache ausgeschlossen werden, da über die genaue Beschaffenheit dieser Ursachen wenig Aussagen möglich sind. Der Beitrag verschiedener Strukturelemente zur Schwere wurde in Kap. 5.4.2. anhand der Abb. 41 abgeschätzt. Hieraus kann bereits der Schluß gezogen werden, daß die Schwellenbildung auf sublithosphärische Ursachen zurückführbar ist.
Modelle, die die Schwellenbildungsmechanismen innerhalb der Lithosphäre sehen, sind
- "underplating"-Basalt bis hinunter zur Basis der Lithosphäre nach Burke und Whiteman (1973),
- "underplating" durch verarmten Peridotit nach Jordan (1979),
- Veränderte Komposition der Lithosphäre nach Haxby und Turcotte (1978) sowie
- "thinning" bzw. "reheating" der Lithosphäre nach Detrick und Crough (1978).
Alle diese Mechanismen laufen auf einen Bereich verminderter Dichte innerhalb der Lithosphäre hinaus und können somit durch das Modell der "altered lithosphere" nach Abb. 54d (Crough, 1983a) dargestellt werden. In Kap. 7.1.2. wird hierauf noch etwas näher eingegangen.
Als mögliche Ursachen im Bereich der Asthenosphäre gaben zuerst Morgan (1971), Menard (1973) und Anderson et al. (1973) dynamische Mantelkonvektionsvorgänge, in die Materialaufstiegsprozesse involviert sind, an. Cochran und Talwani (1978) gehen lediglich von einer anomalen asthenosphären Zusammensetzung und/oder Temperatur aus. Diesen Fall repräsentiert das Modell nach Abb. 54e. Dabei ist hinzuzufügen, daß die anomale Asthenosphäre auch als Folgewirkung von Konvektionsprozessen verstehbar ist. In diesem Sinne spiegeln die Vorstellungen von Cochran und Talwani (1978) und z. B. Morgan (1971) vergleichbare bzw. zusammenhängende Phänomene wider. Gewissermaßen als Synthese derartiger Vorstellungen hat sich mittlerweile die Mantel-Plume-Hypothese, erläutert in Kapitel 2.2.2.1., etabliert. In diesem Sinne kann das Modell nach Abb. 54e stellvertretend für ein nicht näher beschriebenes Mantel-Plume-Modell angesehen werden.
Für eine veränderte Lithosphäre stellt sich die Frage nach deren Ursache. Somit läßt sich die veränderte Lithosphäre als Folge einer Mantel-Plume-Aktivität auffassen, indem eine entsprechende Wechselwirkung zwischen Plume und Lithosphäre stattfindet. Die mögliche Existenz der Mantel-Plume-Struktur folgt auch aus den Ergebnissen seismischer Tomographie, die die Abb. 23 in Kap. 3.3.3. u. a. für den sublithosphärischen Tiefenbereich von ca. 130 km zeigt. Sollte der Mantel Plume existieren und sich an der Oberfläche schließlich durch Vulkanismus bemerkbar machen, kann davon ausgegangen werden, daß dies nicht spurlos am betroffenen Lithosphärenabschnitt vorübergegangen ist. Außerdem muß das aufgebaute Vulkangebäude durch seine Auflast die Kruste derart beeinflussen, daß sie sich gemäß der Balkenbiegetheorie verbiegt. Dies bedeutet schließlich, daß ein vollständiges Mantel-Plume-Hot-Spot-Modell aus einer geeigneten Superposition der Effekte aus den Modellen nach Abb. 54c,d,e zusammengesetzt werden muß.
Die durch eine Superposition gegebenen Kausalzusammenhänge stellen sich folgendermaßen dar. Zunächst kommt es zu einer allgemeinen Aufwölbung der Lithosphäre durch den Plume. Im Rahmen der Wechselwirkung mit der Lithosphäre kommt es zu Vulkanismus an der Oberfläche und dem Auftreten von Bereichen veränderter ("altered") Lithosphäre. Der Vulkanismus führt nun zu einer Beanspruchung der Kruste durch die geschaffenen Vulkangebäude. Deren Auflast führt zu einer Durchbiegung der Kruste, die in mehreren hundert Kilometern Entfernung beiderseits der Vulkankette zu einer Aufwölbung führt. Die regionale Schwelle wird dabei insbesondere durch die veränderte Lithosphäre und den Plume hervorgerufen. Somit stützen sich auch die Modelle nach Abb. 54c,d auf die Existenz der Mantel-Plume-Struktur, die Abb. 54e repräsentiert. Diese Zusammenhänge werden auch anhand von Abb. 69 in Kap. 8.3. deutlich.
Im Rahmen der Modellierung des hawaiianischen Mantel-Plume-Hot-Spots in Kapitel 8 steht die Zielsetzung, eine bessere Evidenz für den in der Literatur diskutierten Mantel Plume zu bekommen. Abgesehen davon kann man aber schon Indizien für die Existenz asthenosphärischer Mantel-Plume-Hot-Spot-Ursachen aus anderen Beobachtungen ableiten. Zu diesen Beobachtungen gehören insbesondere Schlußfolgerungen aus der Plattentektonik. Diese beschreibt die Bewegung lithosphärischer Platten relativ zur Asthenosphäre. Der Mantel-Plume-Hot-Spot von Hawaii liegt im Bereich der sich mit 10 cm pro Jahr bewegenden pazifischen Platte. Damit kann hier klar zwischen lithosphärischen und sublithosphärischen Ursachen unterschieden werden. Die lithosphärischen Ursachen müssen sich mit der Platte fortbewegen, also relativ zur Erdoberfläche ortsfest bleiben. Eine Ortsverlagerung vulkanischer Tätigkeit innerhalb einer Platte läßt auf eine Relativbewegung von Ursache und Plattenbewegung rückschließen. Dies kann durch asthenosphärische Ursachen erklärt werden. Freilich ist damit die Existenz eines Mantel Plumes nicht erwiesen, jedoch liegt diese Interpretation der Beobachtung sehr nahe. Weiterhin dafür spricht das schnelle Absinken der Inseln (Detrick et al., 1977; Detrick et al., 1981). Die Ergebnisse hinsichtlich der Plume-Evidenz aus obigen Überlegungen können auch sinngemäß auf Mantel-Plume-Hot-Spots übertragen werden, in dessen Bereich sich kaum bewegende Lithosphäre liegt, z. B. bei den Kapverden. Auf diesen Gedanken wird in Kapitel 9.3. zurückgekommen.
Bleibt die Frage nach der Ursache zur Bildung der Mantel Plumes oder vergleichbarer Strukturen. Darüber gibt es mannigfaltige Überlegungen in der Literatur, die die Existenz der Mantel Plumes auf verschiedenen Wegen schließlich als Konvektionsphänomen darstellen. Über die genaue Ursache gibt es eine anhaltende Diskussion über Art und Ort der Entstehung. Aber im Rahmen dieser Arbeit reicht es völlig aus, festzustellen, daß die Mantel Plumes als Folge oder Bestandteil der Mantelkonvektion angesprochen werden können. Ein vergleichbares Phänomen existiert auch in der Troposphäre. Die dem Mantel Plume vergleichbare Struktur hinsichtlich Konvektionsströmung und Entstehung an einer Grenzschicht, hier entweder Eigenschaften der Erdoberfläche am thermischen Ursprungsort oder Luftmassengrenzen, ist die Luftmasse im Bereich eines Cumulonimbus mit Amboß. Hier führt die Erwärmung der Erdoberfläche zu einer labilen Temperaturschichtung, die das Aufsteigen der erwärmten Luft begünstigt. Bei Erreichen der Temperaturinversion der Tropopause kommt es auch hier zum seitlichen Auswandern der aufgestiegenen Luftmassen.
7.1.2. Definition der alterierten Lithosphäre
Die von Crough (1983a) angegebene "altered lithosphere" (vgl. Abb. 54d) geht auf eine Reihe von Modellen zurück, in denen die Ursache für Hot-Spot-Schwellen im lithosphärischen Mantel angenommen wird. Neben den bereits in Kap. 7.1.1. angesprochenen Modellen, die die Ursache(n) zur Schwellenbildung innerhalb der Lithosphäre ansiedeln, gehören "lithospheric erosion" nach Ribe und Christensen (1994) und Einbruch von asthenosphärischem Material in die Lithosphäre ebenfalls dazu. In den lithosphärischen Mantel eindringendes asthenosphärisches Material weist eine um mehrere hundert Grad erhöhte Temperatur auf, so daß hierfür im Rahmen der Dichtemodellierung keine typisch asthenosphärische Dichte mehr angesetzt werden kann, sondern vielmehr eine sogar noch die Dichte der Lithosphäre unterschreitende Dichte angesetzt werden muß.
Alle angesprochenen Modelle laufen auf einen metasomatisch veränderten lithosphärischen Mantel, der die "altered lithosphere" nach Abb. 54d darstellt, hinaus. Eine petrologische Abhandlung des genauen Ablaufs metasomatischer Prozesse (siehe z. B. Menzies und Hawkesworth (1987)) führt über den Rahmen dieser Arbeit hinaus. Der metasomatisch veränderte lithosphärische Mantel konnte bei Gran Canaria (Kanaren-Hot-Spot) petrologisch nachgewiesen werden (Hoernle et al., 1991; Hoernle und Schmincke, 1993). Ferner ist den Arbeiten von Hoernle et al. (1991) und Hörnle und Schmincke (1993) zu entnehmen, daß das bei den Kanaren beobachtbare geochemische Spektrum größer ist als an allen übrigen ozeanischen Intraplatten-Hot-Spot-Lokationen (vgl. auch Schmincke et al., 1993) und daß damit auch unter den Hawaii-Inseln der metasomatisch veränderte lithosphärische Mantel nicht so ausgeprägt ist wie bei den Kanaren. Dies wird insbesondere auf die Unterschiede in der Plattengeschwindigkeit (Hawaii: schnelle pazifische Platte; Kanaren: fast ruhende afrikanische Platte) zurückgeführt (persönliche Diskussion mit P. M. Sachs).
In der Arbeit von Glahn et al. (1992) werden für die geothermische Anomalie von Urach petrologische Ergebnisse mit teleseismischen Studien verglichen. Glahn et al. (1992) sehen eine "low-velocity-structure" im lithosphärischen Mantel und interpretieren diese in Zusammenhang mit den petrologischen Untersuchungen als metasomatisch veränderten lithosphärischen Mantel teleseismisch. Somit läßt sich möglicherweise metasomatisch veränderter lithosphärischer Mantel teleseismisch beobachten. Im Falle von Hawaii ist dies bisher nicht untersucht worden.
In Anlehnung an die "altered lithosphere" von Crough (1983a) werden die aufgelisteten Prozesse, die im lithosphärischen Mantel liegende Ursachen der Schwellenbildung darstellen, unter dem Begriff der Alteration der Lithosphäre zusammengefaßt. Insbesondere wird dabei in der vorliegenden Arbeit im folgenden der metasomatisch veränderte lithosphärische Mantel als "alterierte Lithosphäre" bezeichnet. Damit wird hier "altered lithosphere" mit "alterierte Lithosphäre" übersetzt. Die alterierte Lithosphäre stellt somit letztendlich den Bereich des lithosphärischen Mantels dar, der ganz allgemein durch chemische, thermische und physikalische Prozesse so verändert wurde, daß ein (modellierbarer) Dichtekontrast zwischen alterierter und nicht alterierter Lithosphäre zu erwarten ist. Unter Alteration der Lithosphäre werden in der vorliegenden Arbeit damit alle Prozesse angesprochen, die eine Veränderung der (normalmächtigen) Lithosphäre nach sich ziehen.
7.2. Zweidimensionale Dichtemodelle
Der nächste Schritt zu einem dreidimensionalen Mantel-Plume-Hot-Spot-Dichtemodell von Hawaii besteht darin, die Informationen aus Kap. 7.1. zu verarbeiten. Daher wird die Struktur des 3D-Modells sich schließlich aus den Beiträgen der Effekte nach Abb. 54c,d,e zusammensetzen. Somit wird zunächst eine zweidimensionale Betrachtung hinsichtlich der Schwerewirkung der in Abb. 54 gezeigten Fälle durchgeführt. Hieraus ergeben sich dann Hinweise auf die zu verwendenden Größenordnungen für die Dichtemodellierung im dreidimensionalen Fall. Außerdem kann auf diese Weise schon erarbeitet werden, von welchem Effekt wohl welcher Beitrag erwartet werden muß, um die beobachtete Bougueranomalie zu erklären (siehe dazu dann Kap. 7.3.). Aufgrund der nicht vorhandenen Eindeutigkeit gravimetrischer Daten bezüglich der Strukturen soll die Modellvariation mit einem Minimum an verschiedenen Dichten vorgenommen werden.
Zur Vorbereitung der 3D-Modellierung wurde für die 2D-Modellierung die Verlängerung des bereits in Kapitel 5 hinsichtlich des Krustenaufbaus diskutierten Profils senkrecht zum Streichen der Inselkette westlich des aktiven Inselvulkanismus ausgewählt, so daß der Bereich der regionalen Schwelle erfaßt wird. Da es nun um die Modellierung tiefer gelegener Ursachen größerer Wellenlängen geht, wird die genaue Krustenstruktur aus Kap. 5 zu einer mittleren Krustendichte von 2,95 g/cm3 zusammengefaßt. Damit wird nicht mehr zwischen Sedimenten, Vulkanbauten und darunterliegender ozeanischer Kruste differenziert. Nach Abb. 38 wird die ozeanische Kruste mit einer Dichte von 3,0 g/cm3 modelliert. Da aber die oberen Schichten, Sedimente und vulkanische Förderprodukte geringere Dichten aufweisen, wurde in der vorliegenden Arbeit mit dem reduzierten Wert von 2,95 g/cm3 gerechnet.
Die Krusten-Mantel-Grenze ist als die sogenannte Mohorovicic-Diskontinuität ("Moho") durch die plötzliche Zunahme der seismischen p-Wellengeschwindigkeit definiert. Die in diesem Sinne vorliegende seismische Definition der "Moho" trennt das Krustengestein Gabbro ( = 3,0 g/cm3) vom Mantelgestein Peridotit ( = 3,3 g/cm3). Der Zustand beider Stoffe ist fest. Die Krusten-Mantel-Grenze stellt somit eine auf seismische Weise definierte Unstetigkeit dar.
Die Grenze zwischen der Lithosphäre und der Asthenosphäre dagegen kann nicht in Form einer auf physikalischem Wege definierbaren Unstetigkeit festgelegt werden. Die Lithosphäre umfaßt die gesamte Erdkruste mitsamt dem obersten Mantel. Genaue Definitionen der Lithosphäre wurden bereits in Kap. 3.3.2. diskutiert. Der Übergang von der Lithosphäre zur Asthenosphäre wird nicht durch eine Unstetigkeit markiert, sondern ist unscharf.
Die in Abb. 38 angegebene Dichte für die der Kruste angrenzenden Mantelbereiche von 3,33 g/cm3 stellt einen Mittelwert des oberen Mantels dar, im Rahmen der Modellierung wird hier jedoch mit dem Wert von 3,28 g/cm3 gearbeitet. Dieser Wert ist Toksöz (1985) für die Lithosphäre entnommen. Für die Asthenosphäre gibt Toksöz (1985) für den Tiefenbereich bis 150 km die Dichte 3,34 g/cm3 an. Für größere Tiefen bis ca. 230 km gibt Toksöz (1985) einen Dichtewert von 3,38 g/cm3 an. Mit zunehmender Tiefe erhöht sich die Dichte weiter. Dies ist jedoch nicht weiter von Bedeutung für die Modellrechnungen: Der sublithosphärische Pilz eines Mantel Plumes liegt im Bereich der oberen Asthenosphäre. Da vor allem die Dichtedifferenz von Plume zu ungestörter Asthenosphäre von Wichtigkeit ist, wird die Asthenosphäre mit einer in diesem Bereich mittleren Dichte von 3,36 g/cm3 dargestellt.
Die Angaben für Dichten von Peridotit und Gabbro in der Literatur (siehe z. B. Gebrande (1982)) sowie Dichte-Tiefen-Diagramme (vgl. z. B. Bott (1982) sowie Bursa und Pec (1993)), die die Zunahme der Dichte mit der Tiefe aufzuzeigen versuchen, führen dazu, die Asthenosphäre mit einer größeren Dichte als die Lithosphäre zu belegen. So zeigen z. B. Brinkmann (1984), Tabelle 35 auf Seite 252, und Toksöz (1985) die Werte von 2,6 g/cm3 bis 3,0 g/cm3 für die Kruste, von 3,24 g/cm3 bis 3,3 g/cm3 für die Lithosphäre und ab bzw. 3,34 g/cm3 für die Asthenosphäre. Der Dichtezunahme mit der Tiefe steht bei Hot Spots und Ridges aber in die Lithosphäre eindringendes, heißes Asthenosphärenmaterial, das eine gegenüber der kalten Lithosphäre verminderte Dichte aufweist, entgegen. Diese temperaturbedingte Dichteerniedrigung jedoch müßte dann größer sein als der oben angegebene Dichtekontrast von Asthenosphäre und Lithosphäre. Nach Brinkmann (1984), Seite 254, ist die Dichte der Asthenosphäre in den Ozeangebieten ohnehin geringer als die der Lithosphäre. Dem "Preliminary Reference Earth Model (PREM)", dargestellt in Dziewonski und Anderson (1984), liegt kein großer Dichtegradient zwischen Lithosphäre und Asthenosphäre zugrunde. Nach Dziewonski und Anderson (1984) nimmt die Dichte zwischen dem lithosphärischen Mantel ("Lid") und der darunter liegenden "low-velocity-zone" der Asthenosphäre leicht ab.
Um den Einfluß der Bathymetrie herauszubekommen, wird der Wasserkörper mit eben der Krustendichte, hier 2,95 g/cm3, aufgefüllt. Als Ergebnis liefert dies die Bouguerschwere. Der in Kapitel 5 diskutierte Sillkomplex (subkrustaler Intrusivkörper) kann aufgrund seiner lediglich lokalen Bedeutung ebenfalls vernachlässigt werden. Modelliert wird schließlich eine unter der Auflast der Inselkette nach der Balkenbiegetheorie deformierte Kruste. Die Kruste weist eine gleichmäßige Mächtigkeit auf. Dadurch wird die in die Geometrie der Kruste übernommene regionale Meeresbodentopographie parallelverschoben auch als Krusten-Mantel-Grenze wiedergegeben. Zusammen mit der für die Lithosphäre zugrundegelegten Dichte von 3,28 g/cm3 ergibt sich zwischen Kruste und Mantel ein Dichtekontrast von 0,33 g/cm3. Die in Abb. 55 gezeigte Bougueranomalie der Krusten-Mantel-Grenze spiegelt in ihrer Form den Verlauf der Tiefenlage dieser Grenze wider. Es ist klar zu erkennen, daß lithosphärische Überschußmassen im Bereich der Krustenaufwölbung liegen. Die eingetauchten Krustenbereiche liefern ein lokales Bouguerminimum. Auf regionaler Ebene liegt aber ein Bouguermaximum vor. Auf die Verteilung von relativen Dichteanomalien (Überschuß- und Defizitmassengebiete) wird in Kap. 8.3. noch genauer eingegangen.
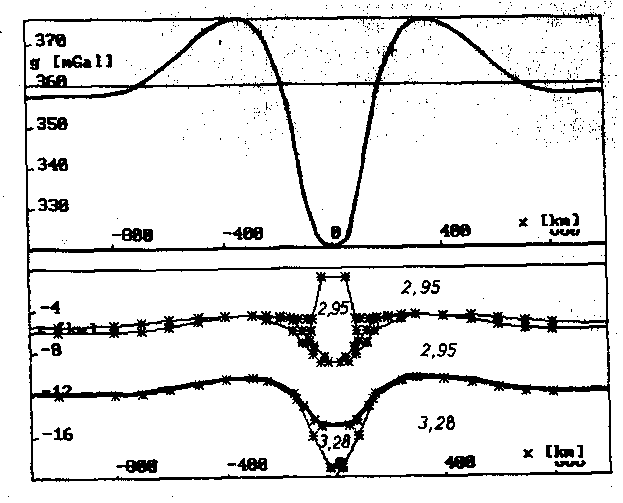
Abb. 55. Schweresignal der Krusten-Mantel-Grenze. Die angegebenen Dich-
ten sind in g/cm
Bei einer für die Asthenosphäre angenommenen Dichte von 3,36 g/cm3 liegt dann die Dichte der Mantel-Plume-Struktur nach Kap. 5.4. bei dem reduzierten Wert von 3,34 g/cm3. Ferner wird für die alterierte Lithosphäre (vgl. Kap. 7.1.2.) zunächst ein Wert von 3,25 g/cm3 eingesetzt, der gegenüber dem Wert für die ungestörte Lithosphäre um 0,03 g/cm3 vermindert ist. Weiterhin wird die Lithosphäre im zentralen Bereich über dem Mantel Plume leicht angehoben, um den Einfluß aufsteigender Konvektion auf eine Sperrschicht zu berücksichtigen. An dieser Stelle sei erwähnt, daß in klassischen Plume-Modellen die gesamte Lithosphäre über dem Plume angehoben wird. Würde das der Fall sein, müßte aufgrund überall vorhandener Überschußmassen (die jeweils dichtere Schicht ist hochgebogen) eine positive Bougueranomalie festzustellen sein. Dies ist jedoch nicht der Fall, so daß ein alleiniges Aufwölben der Lithosphäre im Plume-Bereich nicht in Frage kommt und daher an dieser Stelle zunächst in den Hintergrund tritt. Dieser Aspekt wird jedoch später im Rahmen der 3D-Modellierung erneut aufgegriffen und dort genauer behandelt. Die geometrischen Abmessungen für den Mantel Plume werden aus Kap. 5 übernommen. Dem angepaßt ist der Bereich alterierter Lithosphäre. Auf diese Weise ergeben sich die Geometrien der Körper in den Abb. 56 und Abb. 57. In Abb. 56 wird lediglich der Körper der alterierten Lithosphäre modelliert, in Abb. 57 lediglich der Mantel-Plume-Einfluß.
Die Bouguerschwere der alterierten Lithosphäre nach Abb. 56 weist ein deutliches regionales Minimum auf, daß in seiner Größenordnung das regionale Maximum aus der Krustenaufwölbung mehr als ausgleicht. Das eingelagerte deutlich schwächere Maximum ist auf die geringfügige Aufwölbung im zentralen Bereich der Lithosphären-Asthenosphären-Grenze zurückzuführen.
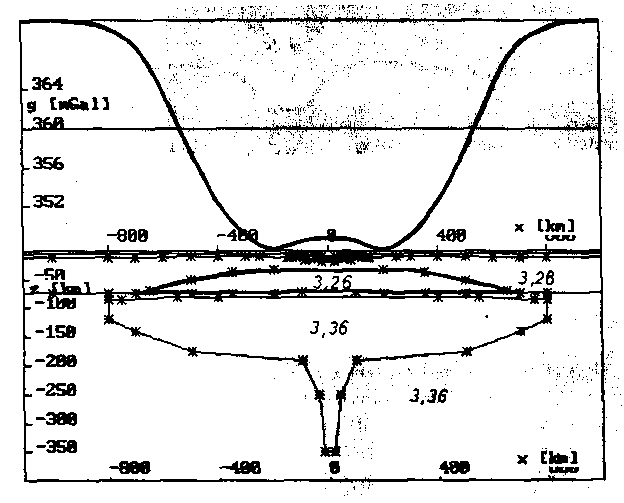
Abb. 56. Schweresignal alterierter Lithosphäre der gezeigten Ausdehnung.
Die angegebenen Dichten sind in g/cm
Die mit einer weitaus dominanteren negativen Bougueranomalie assoziierbare Struktur ist der Mantel Plume im sublithosphärischen Bereich nach Abb. 57. Die hier modellierte Plume-Struktur erzeugt eine signifikante, regionale negative Bougueranomalie. Der genaue Verlauf der Anomalie wird im zentralen Bereich noch durch einen eingelagerten Aufstiegsbereich derart beeinflußt, daß das Extremum schärfer heraustritt. Die in Abb. 57 gezeigte Mantel-Plume-Bougueranomalie stellt eine Möglichkeit unter vielen dar. Zwar variiert die genaue Form der Anomalie mit der Form, Dichte und der Tiefenlage des Mantel Plumes. Aber die Größenordnung der Anomalie läßt sich hiermit aufzeigen. Überlegungen zur Isostasie bezüglich der einzelnen Beiträge der verschiedenen Strukturelemente werden in Kap. 9.2. aufgegriffen.
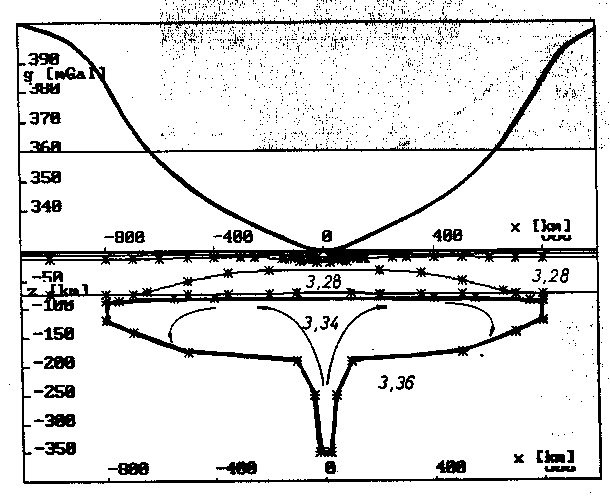
Abb. 57. Schweresignal der Mantel-Plume-Struktur. Die angegebenen Dich-
ten sind in g/cm
7.3. Der Vergleich von Modell- und Bouguerschwere
Aus den vorangegangenen Überlegungen ergeben sich die folgenden Beiträge zur Gesamtbouguerschwere des Modells (vgl. auch Abb. 69 in Kap. 8.3.):
- regionale positive Anomalie aus der Krustenaufwölbung,
- lokale negative Anomalie aus der Wirkung der vulkanischen
Auflast (Durchbiegung),
- regionale negative Anomalie aus alterierter Lithosphäre,
- geringe positive Anomalie aus der Aufwölbung der Lithosphären-
Asthenosphären-Grenze,
- große regionale negative Anomalie aus einer Plume-Struktur.
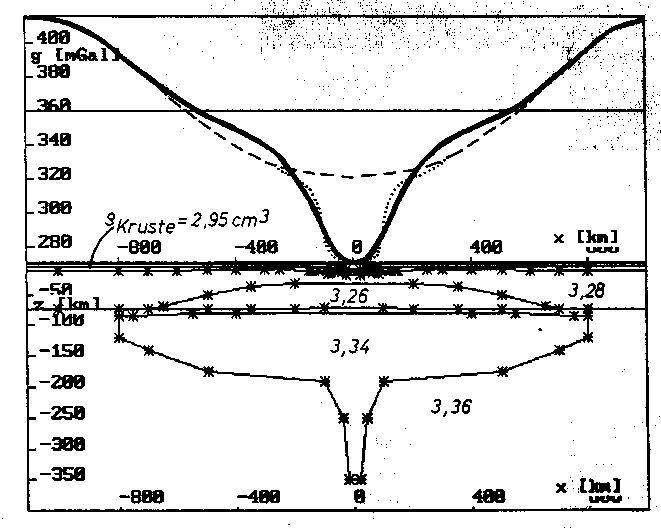
Abb. 58. Superposition der Schwerewirkung von Krusten-, Lithosphären-
und Mantel-Plume-Strukturen, ein Gesamtmodell. Vergleich von
gemessener (gestrichelte Linie mit gepunkteter Linie im Zen-
trum), gefilterter (gestrichelte Linie) und modellierter Bou-
guerschwere (durchgezogene dicke Linie). Dichteangaben sind in
g/cm
Die Superposition dieser Anomalien führt auf die in der Abb. 58 dargestellte Modellbouguerschwerekurve. Danach liefert das Modell sowohl ein regionales als auch ein lokales Bouguertief. Dabei ist das regionale Tief auf die Wirkung der tieferen Strukturen zurückführbar, das lokale Tief eher auf die unter der Vulkanauflast eingesunkene Kruste.
Die zum Vergleich angegebenen ungefilterten Bouguerdaten entstammen der Abb. 51, die der regionalen Bougueranomalie aus Abb. 52. Den jeweiligen Karten wurden dabei die Werte längs der gedachten Profillinie entnommen. Der Vergleich von beobachteter und modellierter Bouguerschwere zeigt eine gute Übereinstimmung in Amplitude und Wellenlänge der Anomalien. Daher können diese Ergebnisse als Grundlage einer 3D-Modellierung verwendet werden.
zurückblättern: vorheriges Kapitel
vorwärtsblättern: nachfolgendes Kapitel
Inhaltsverzeichnis
zur Begrüßungsseite